🚀 Become a Verified Author on Trending Hub24
✍️ Author Account Available @ $60 / Month | +91 7355993756
what is the difference between tree and graph data structure
A tree is a hierarchical data structure that consists of nodes connected by edges, and a graph is a more general data structure compared .
Table of Contents
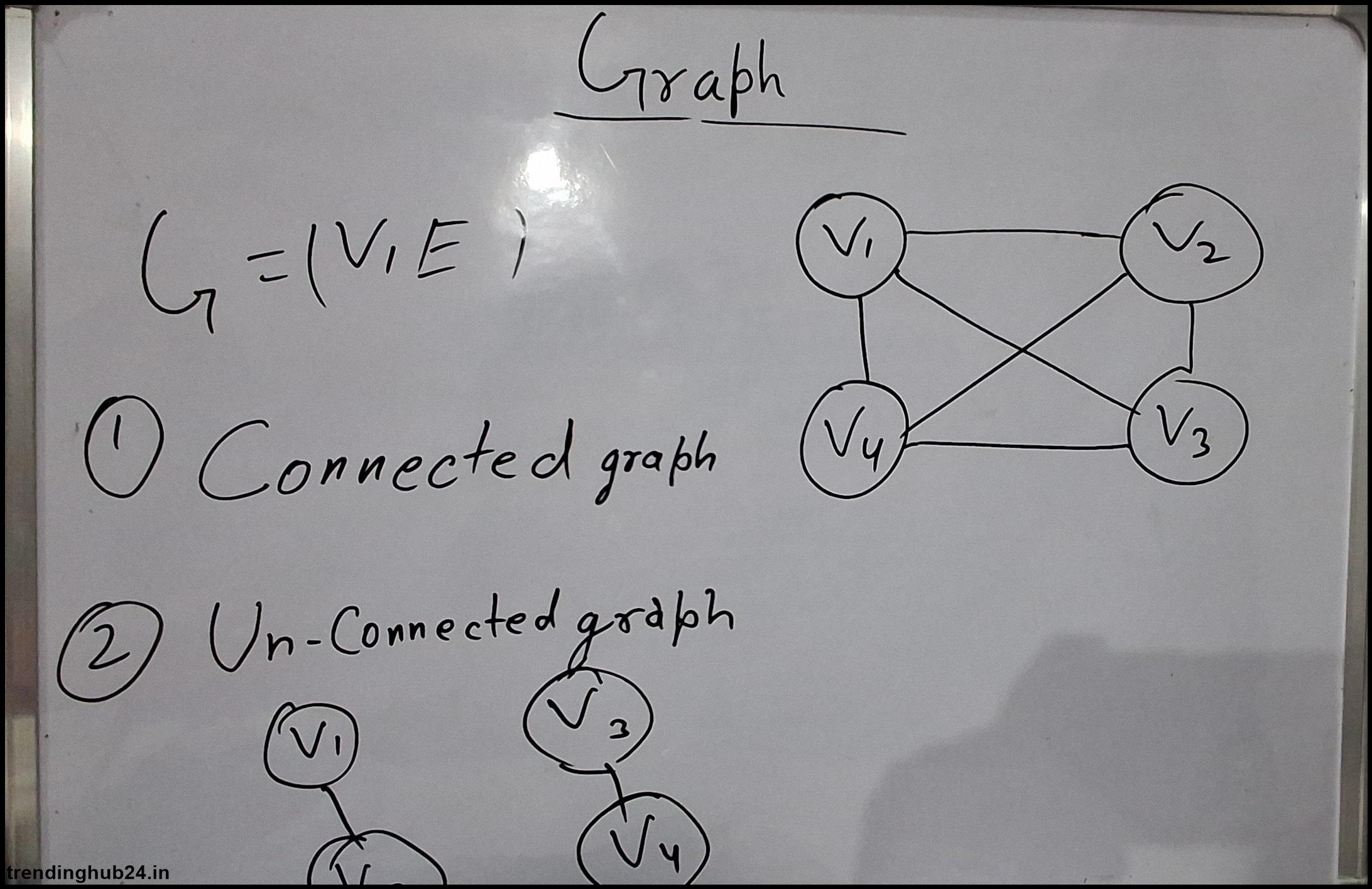
Both trees and graphs are types of nonlinear data structures. They differ from each other in the method of loop construction and type of connection. In other words, a connected tree structure can never contain loops, whereas a graph structure runs on network patterns and can contain loops.
A tree is a hierarchical data structure consisting of nodes connected by edges, and a graph is a more general data structure than a tree, representing complex relationships between objects. In this blog, we will explain their differences in detail!
A graph is a basic data structure in various computations and mathematics, consisting of nodes (or vertices) and a set of vertices that form relationships between these nodes. Graphs are used to represent connections and relationship networks between objects, which makes them valuable in various computer algorithms, network analysis, and social network design.
Trees and graphs are important factors in the world of programming and are non-linear representations of data. Trees are a special example of non-recursive graphs. A graph can have loops. Both graphs and charts share some common characteristics. But there are some differences. Let's explore the difference between a tree and a graph.
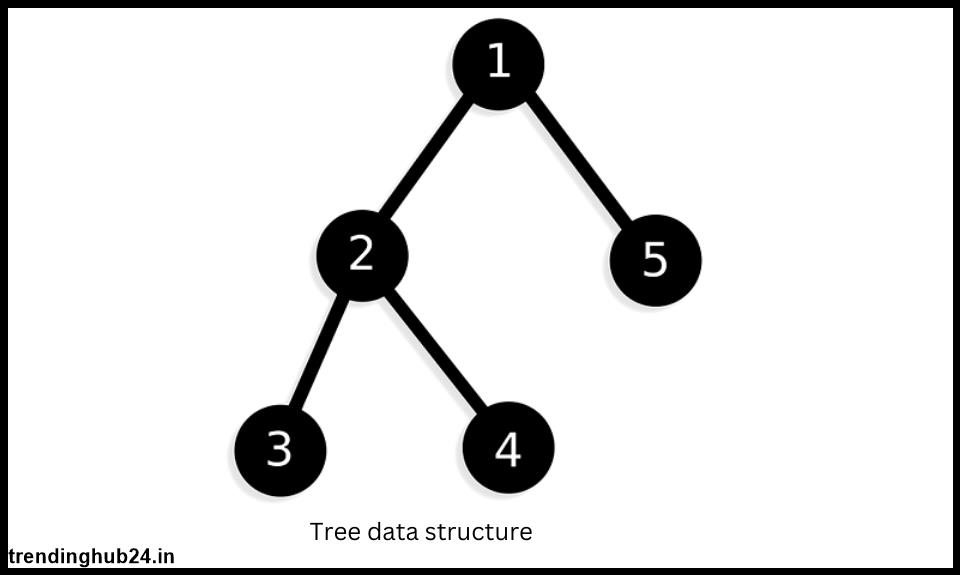
What a tree -
In the world of computing, a tree is known as a hierarchical and non-linear data structure that directly hierarchically stores data.
What is a Graph? -
In the computer science world, a graph is generally known as a nonlinear structure used to represent the flow of calculations. It’s in knots and corners.
Although a tree is a type of graph, there are important differences between tree and graph data structures -
While a tree is a vertical structure, a graph is an example of a network.
A tree has only one path between two nodes, but there are graphs with indirect paths between nodes.
Tree and graph data structure
What is a tree data structure
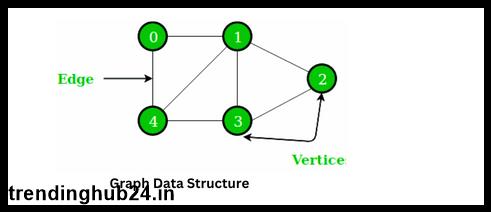
Buds (or Nodes): Buds represent elements or data points in a graph. The set of vertices in a graph is usually called V. Each vertex can have zero or more connections to any other vertices in the graph.
Edge: An edge is a connection between two sides and represents a view or relationship between them. The set of edges of a graph is usually defined as E. Edges can be indirect (two-way) or straight (one-way), and vertices can connect (loop).

Weight (optional): In a weighted graph, each edge can have an associated weight or cost that represents a degree of connectivity or relationship (such as distance, time, or ability). A graph without edge weights is considered unweighted.
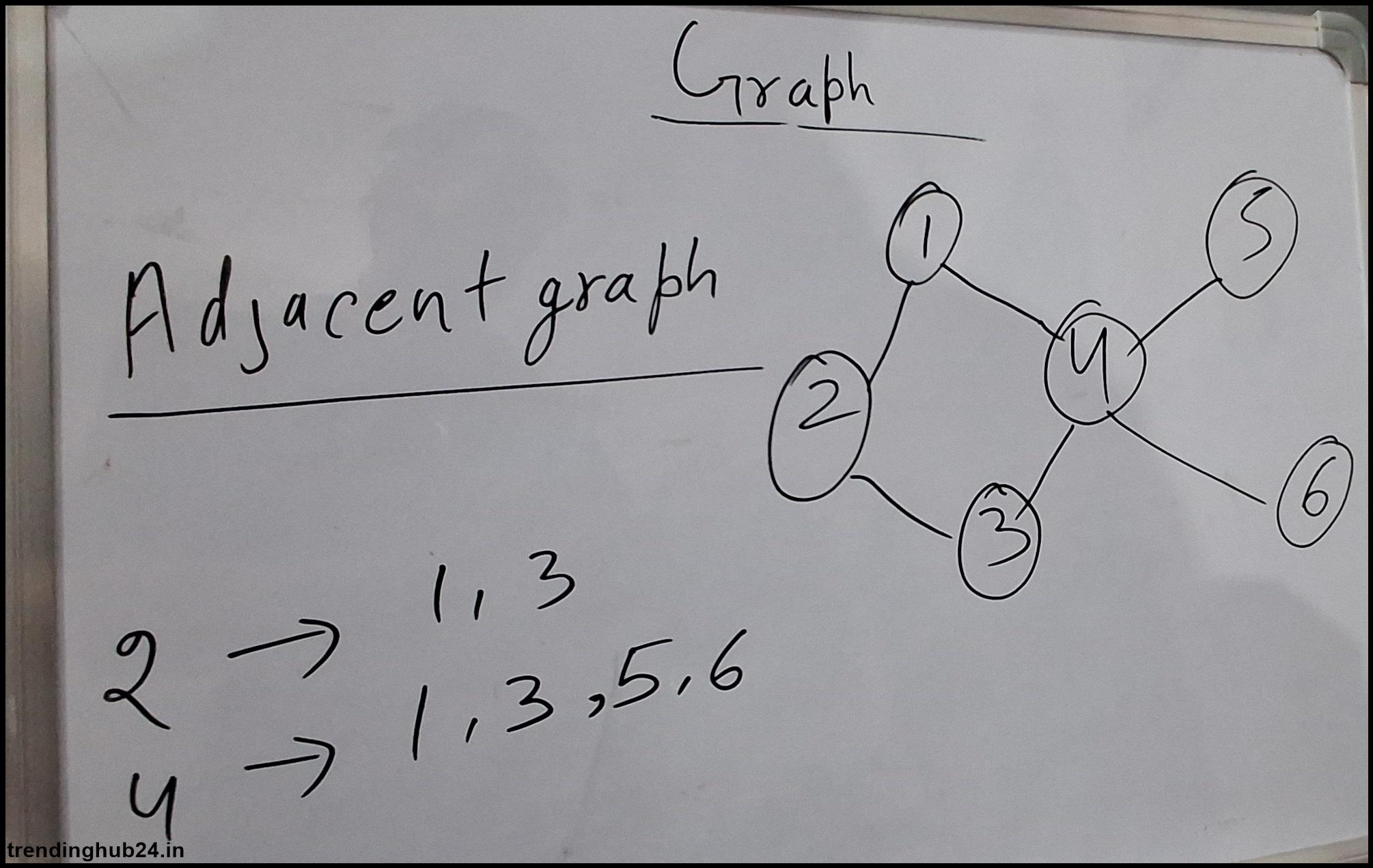
Adjacency: Two vertices are considered adjacent if they are connected by an edge Two edges in an identical vein are adjacent if they share an identical vertex.
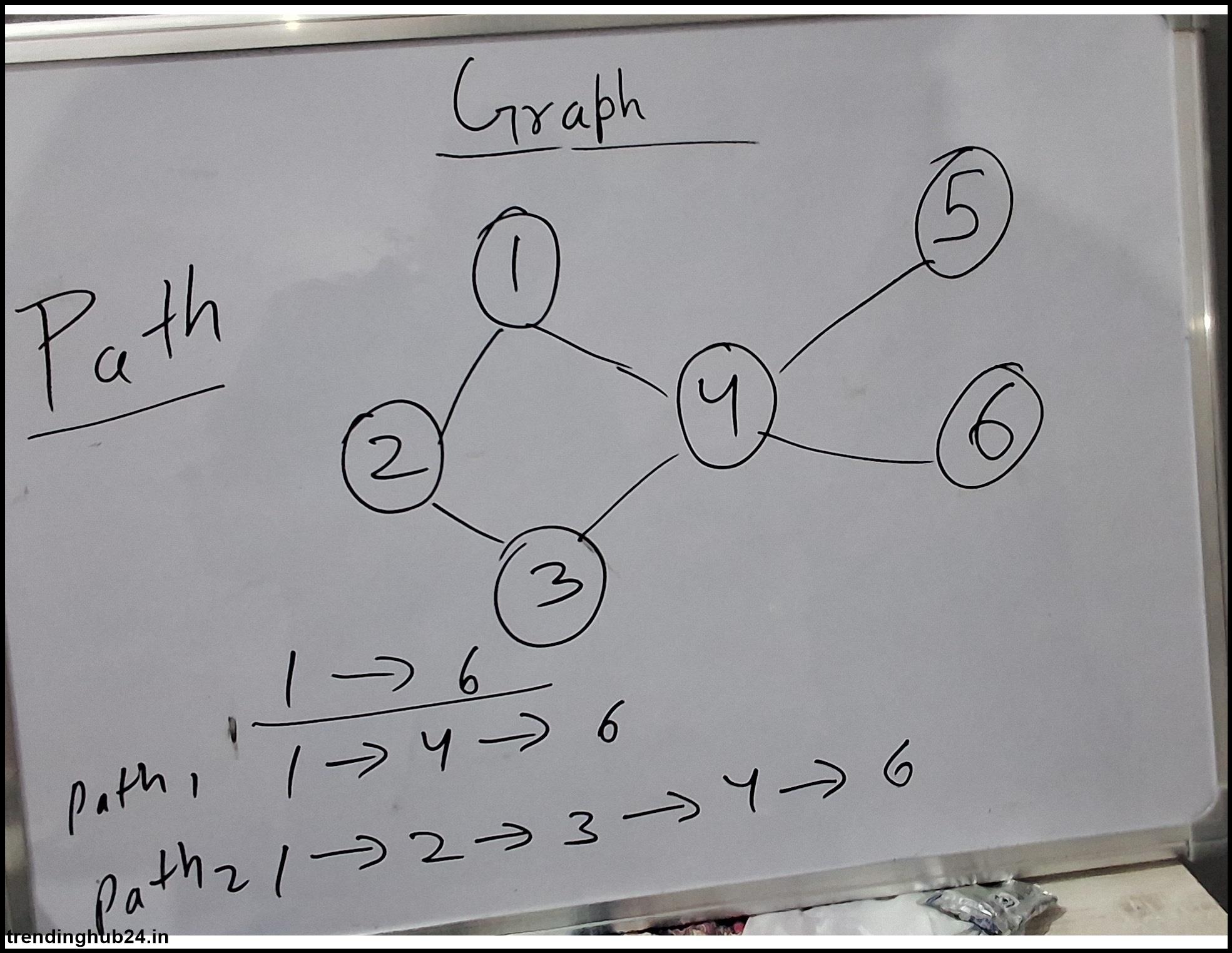
Path: A path is a list of vertices of a graph where all vertices are connected by an edge. In a directed graph, a path follows the path of edges.
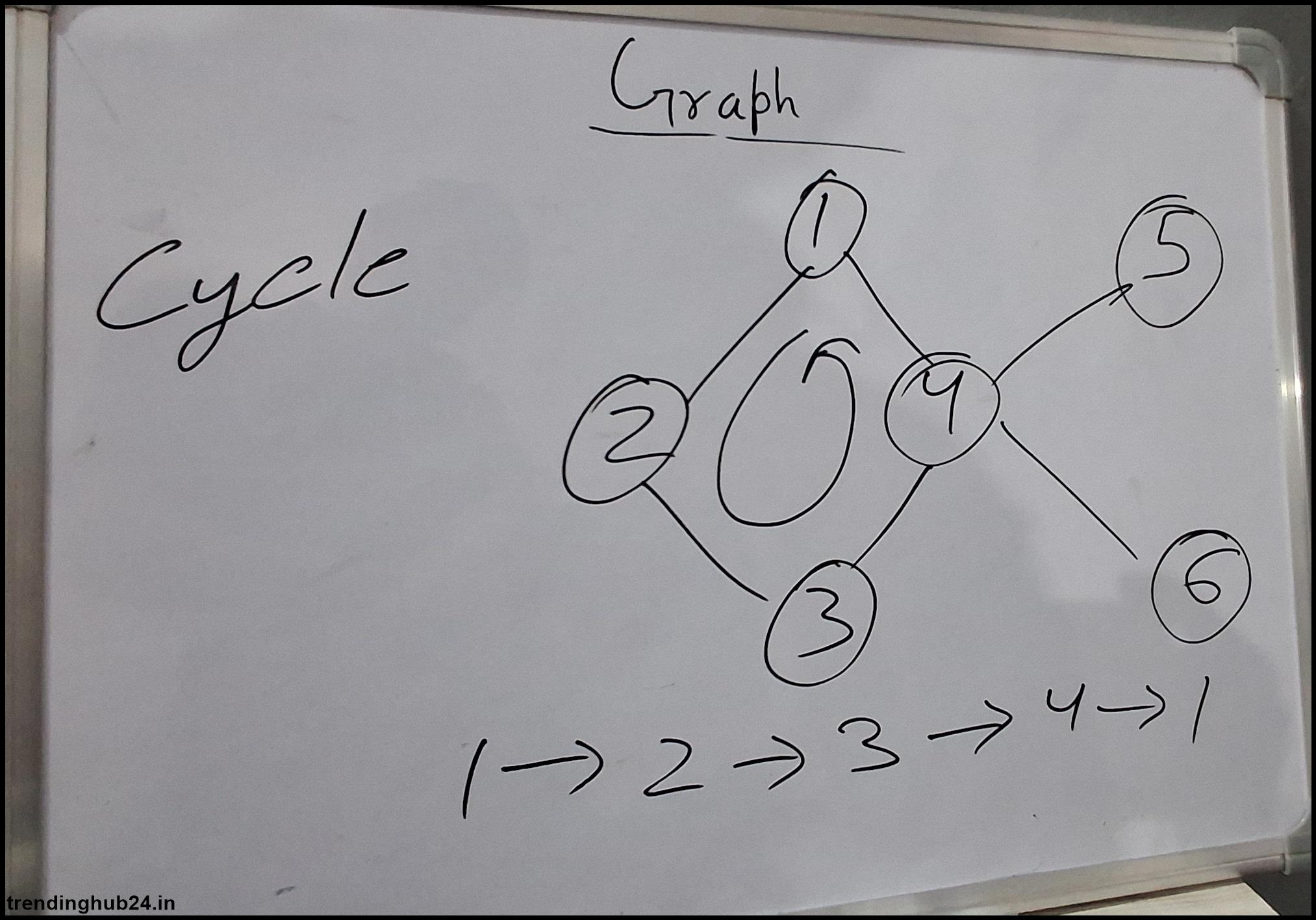
Cycle: A cycle is a path that starts and ends at the same point and indicates all edges and vertices (except the start/end point). Direct imaging, they are called direct curves.
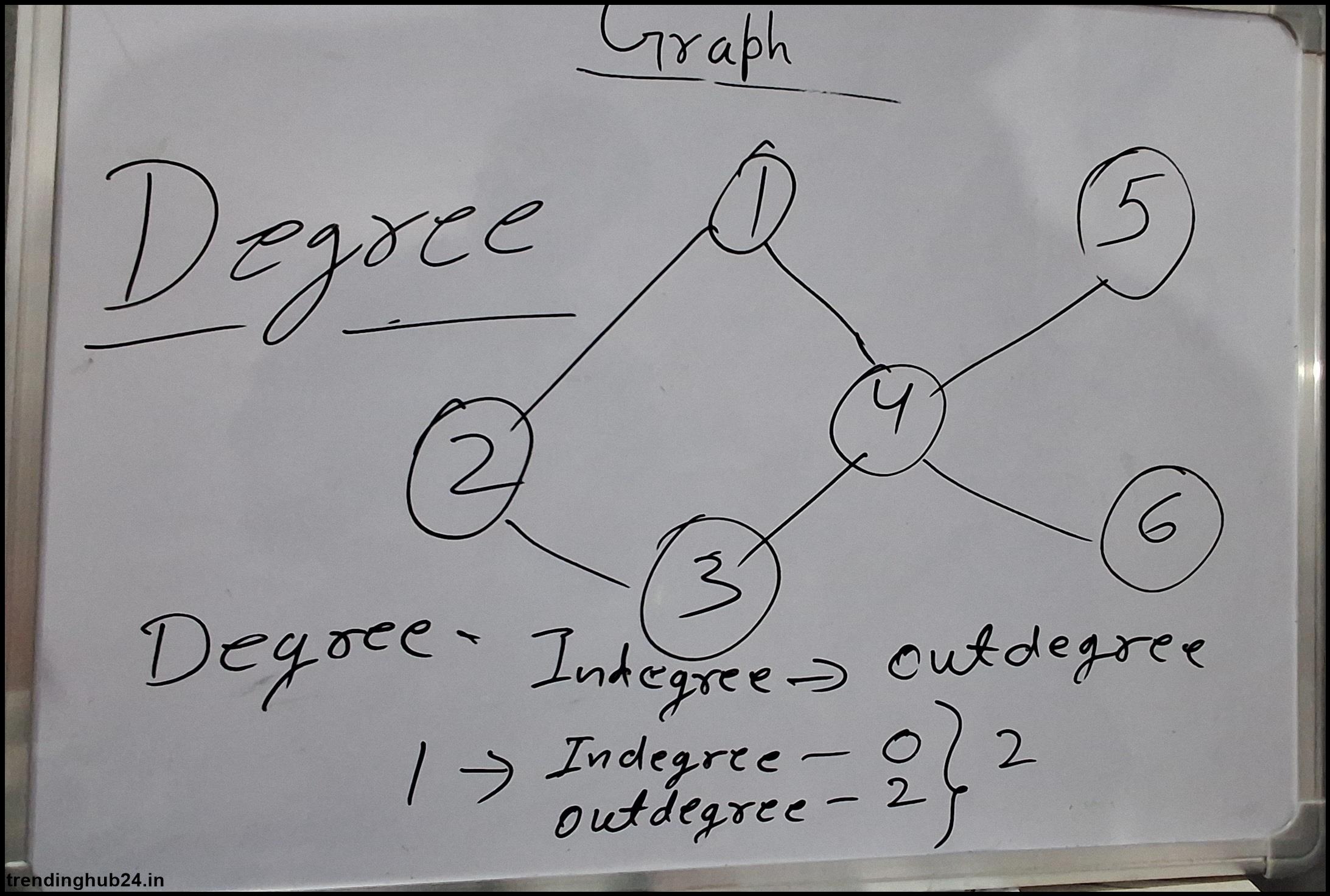
Degree: In a tree data structure, the total number of child nodes is called the node degree. The highest point of all nodes in the tree is called the rank of the tree.
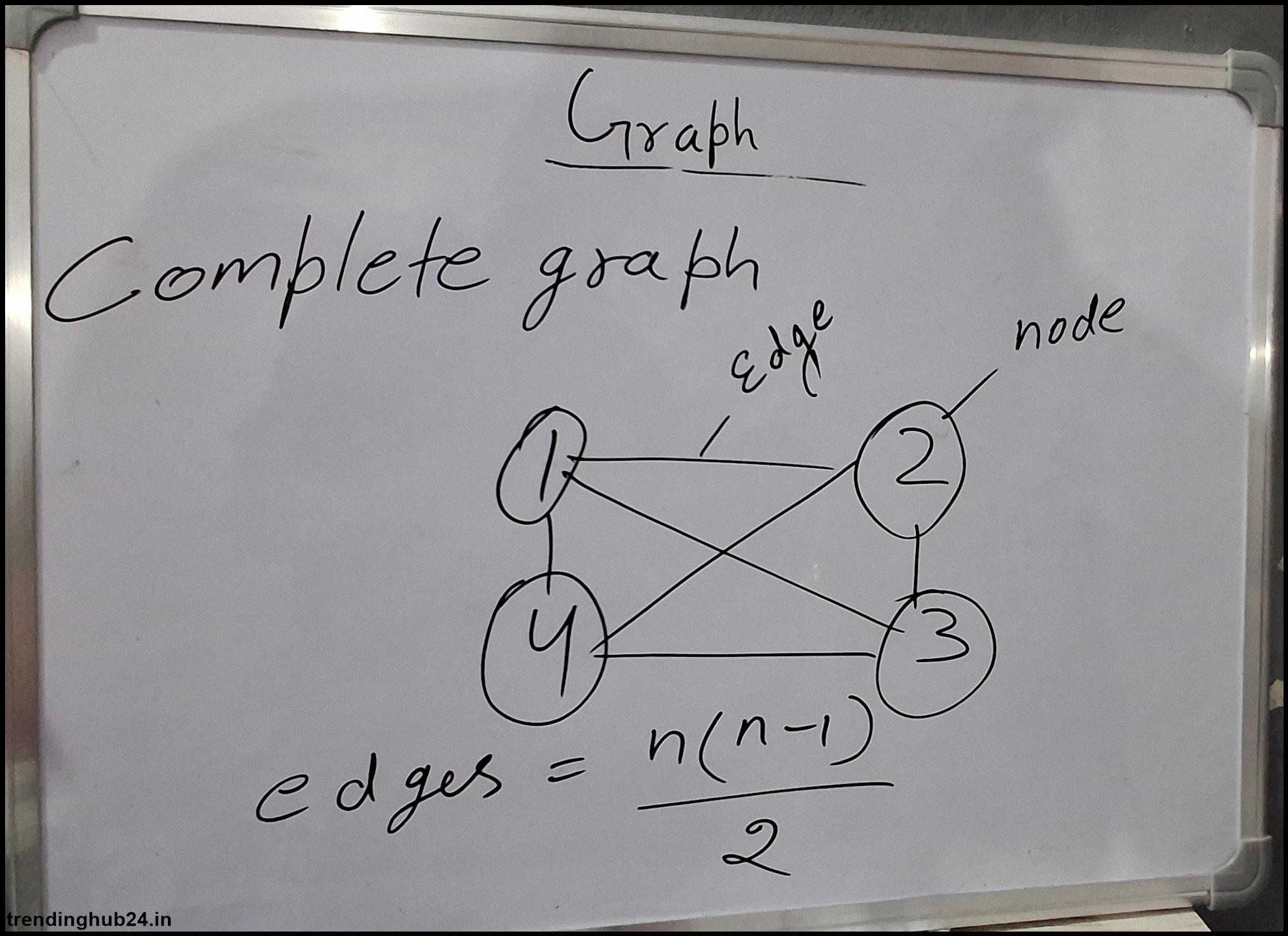
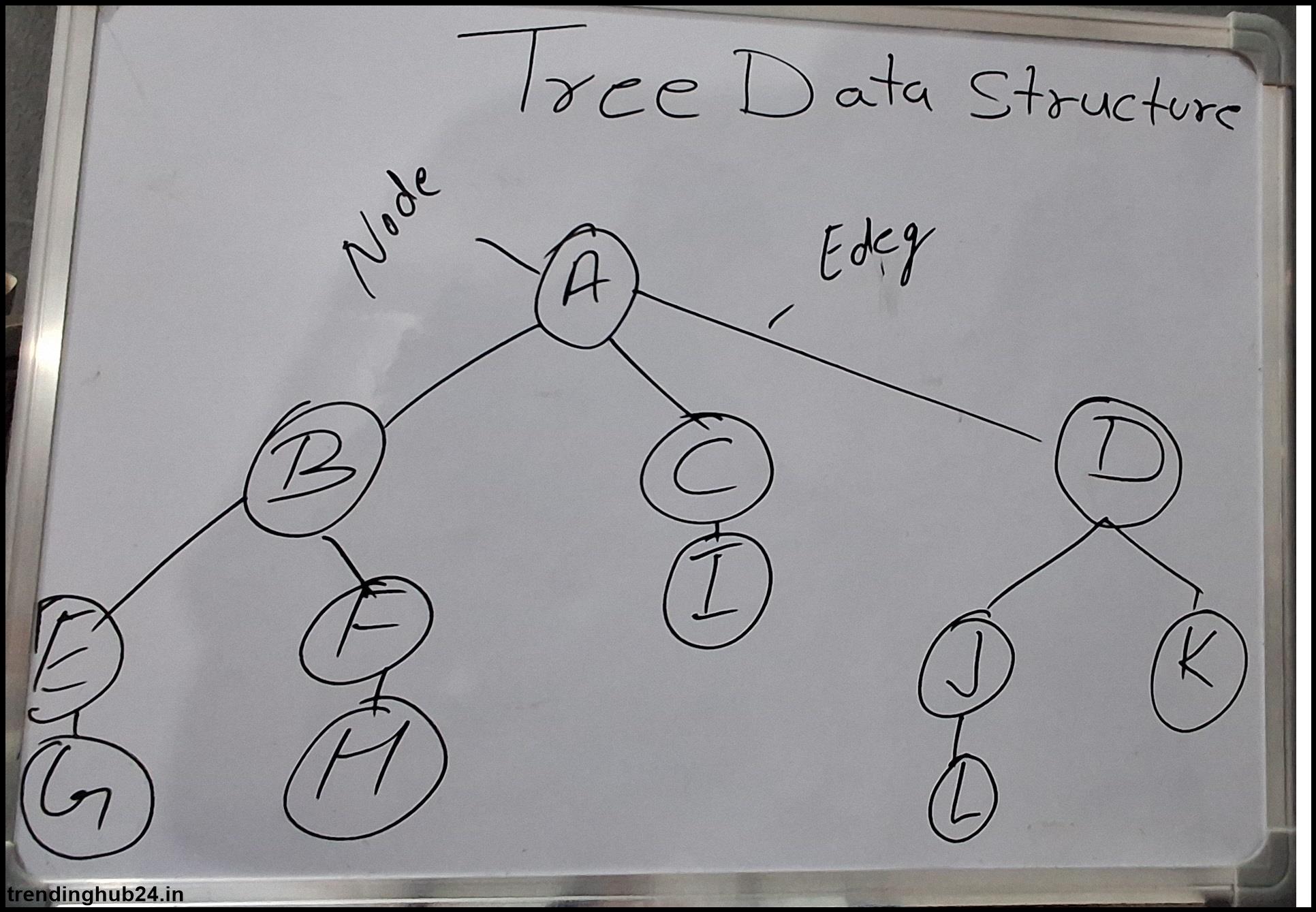
A tree is a primitive network used in computer science and information theory that follows a hierarchical tree structure consisting of a set of connected nodes. This is an important feature of the graph; Specifically, it is an acyclic-connected graph where a node is chosen as the root.
Note: The basic unit of a tree that represents tree elements or data points. Each point can contain data and can be linked to other points (its children).
Path: A series of nodes and edges connecting a network. There is only one way to connect each node in the tree.
Node level: Number of children in a node. In a binary tree, a point can have 0, 1, or 2 degrees.
Tree height: The greatest depth between all nodes in the tree. This is the length of the long path from the root to the leaf.
Root: The top of the tree from which all other branches descend. A root is a part of a tree that has no parents.
| Property | Tree | Graph |
| Definition | A tree is a structure with nodes, one node is called the root, and all other nodes are connected to its sides, so there is a path between any two nodes. | A graph is a set of nodes (vertices) and edges that connect pairs of nodes. Graphs can be used to show multiple relationships between nodes. |
| Cycle | Trees have no curves. A cycle occurs when a path goes from one node to another without returning to the same node. | Graphs can contain cycles that allow a path to be drawn from a node to itself. |
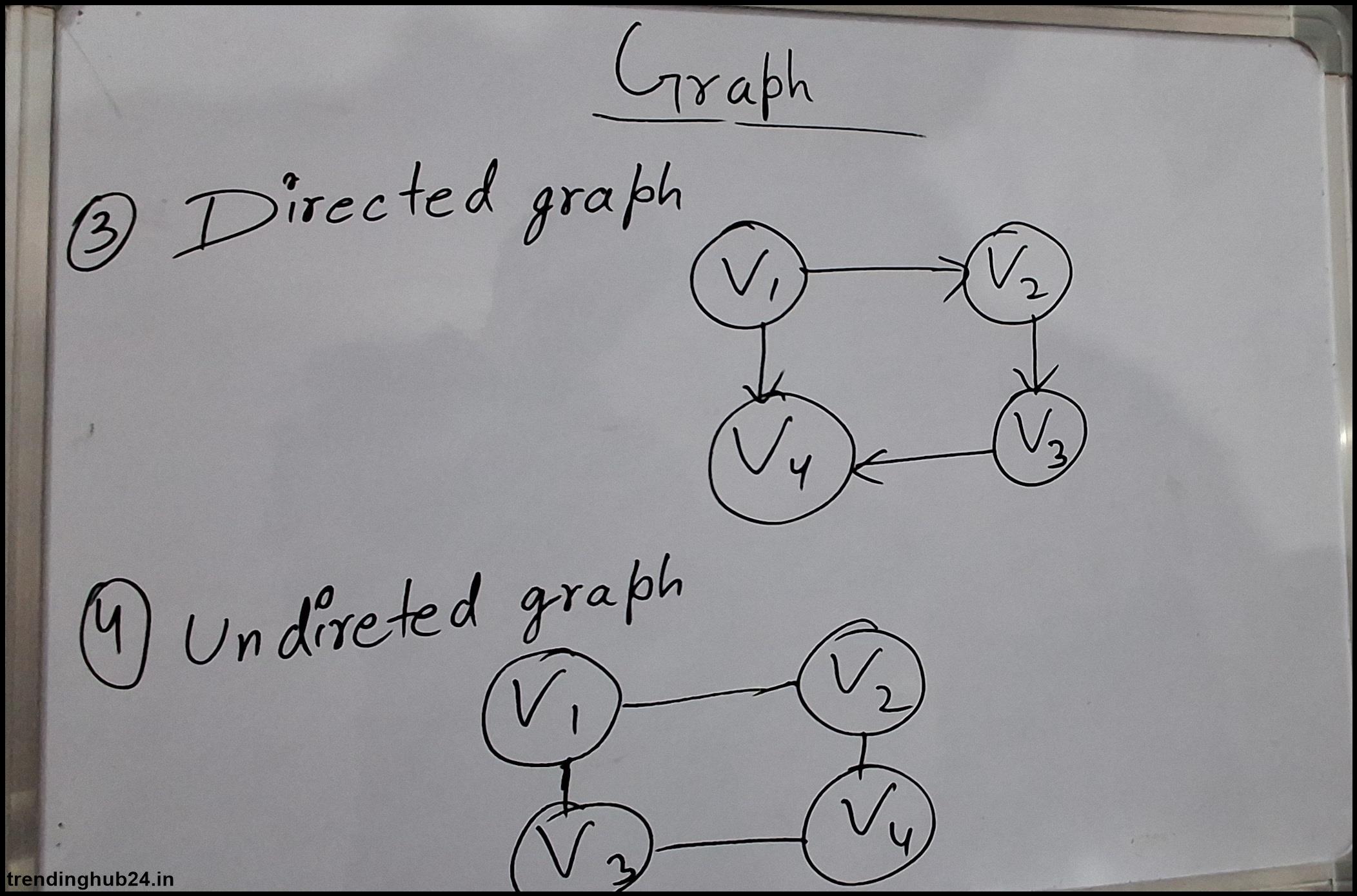
| Direction | Trees cannot have direction or direction. In directed trees (or rooted trees), edges have only one direction. It is usually far from the roots. | Graphs are directed (arc) and undirected. Directed graphs have an edge (point-to-point), while undirected graphs do not. |
| Root | A tree has a single root node from which all nodes descend. | The graph has no root node. Any node can be connected to any other node without requiring a hierarchical structure. |
| Connectivity | In a tree, every two nodes are connected by one path. | A graph can have any number of edges, and the number of edges is not directly related to the number of nodes. |
| Edge Count | A tree shows a branching system where each node (except the root) has only one parent | Graphs can represent complex networks with each branch A node can have zero, one, or more parents |
| Branching | Trees exhibit a branching structure, where each node (except the root) has exactly one parent. | Diagrams can represent complex networks without specific branching patterns. Nodes can have zero, one or more parents. |
| Examples | Family trees: organizational charts and directory structure. | Family Medicine: Organizational Charts and Guidance Forms. |